An Exact Classical Model for TOCSY Transfer in Systems of Three Isotropically Coupled Spins 1/2
R. Marx, S. J. Glaser, Journal of Magnetic Resonance 164, 338-342 (2003).
Quantum phenomena are often highly counter intuitive and classical analogues are known only for a small number of simple quantum systems. A famous example is the Feynman-Vernon-Helwarth theorem which states that the behavior of any quantum mechanical two-level system can be modeled by classical torque equations, i.e. there is a one-to-one correspondence between the dynamics of a two-level system and the dynamics of a spinning top. A single spin 1/2 in an external magnetic field is a prototype example for this analogy. Here we present a classical model that quantitatively reflects the dynamics in an ensemble of up to three isotropically coupled spins 1/2 with arbitrary coupling constants and coupling topology.

The so-called TOCSY experiment (Total Correlation Spectroscopy) was introduced by Lukas Braunschweiler and Richard Ernst in 1983. Since then, it has become one of the most widely used experiments in the field of nuclear magnetic resonance. Especially when large molecules such as proteins are investigated, it provides valuable information about the coupling network formed by nuclear spins. This information helps to identify the individual resonance frequencies of the nuclear spins and ultimately to determine the three-dimensional structure of a molecule.
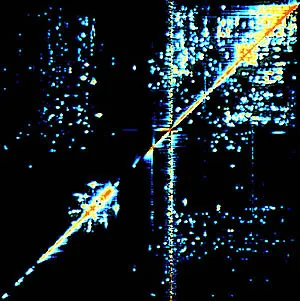
The information provided by a TOCSY spectrum is contained in the dots which are symmetrically located around the diagonal. These so-called cross peaks correlate the frequencies of spins which are part of a common coupling network. The key feature of the TOCSY experiment, which gives rise to these cross peaks, is its ability to efficiently transfer magnetic polarization between coupled nuclear spins. This polarization transfer takes place during a so-called mixing period and choosing the duration of this mixing period properly is a critical step: When is the maximum amount of polarization transfered from a given spin to a desired target spin and how much transfer is to be expected for a given coupling network? However, for coupling networks consisting of more than two coupled spins, the dynamics of polarization transfer is complicated. So far, it was necessary to solve a set of abstract mathematical equations or to resort to computer simulations in order to predict the transfer dynamics of a given spin system and to choose the best mixing time.
However, a possible alternative was already suggested in the seminal paper by Richard Ernst, in which he stated that "the situation is to some extend analogous to a network of coupled mechanical oscillators", i.e. a system of coupled pendulums which all have the same oscillation frequency. However, until recently it was not clear to what extend this analogy holds if the quantum mechanical system and the classical mechanical systems are compared quantitatively for more than two coupled spins. To our surprise, we found that three coupled pendulums not only form a qualitative analogy of the behaviour of three isotropically coupled nuclear spins but in fact closely match all aspects of polarization and coherence transfer. This match becomes perfect in the limit, where the oscillations of the individual pendulums are much faster than the energy transfer between the pendulums.
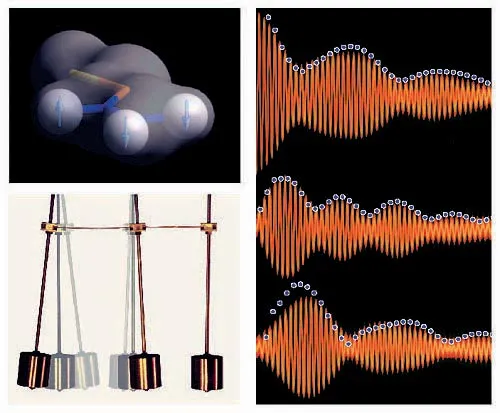
The figure shows the experimental transfer dynamics of polarization in the nuclear spin system formed by the hydrogen atoms of the molecule vinyl magnesium bromide (schematic representation in top left panel) and the transfer of energy in a corresponding set of three coupled pendulums (bottom left panel). The red curves in the right panel are photographic traces of the oscillations of the set of three coupled pendulums. The matching blue circles represent experimentally determined polarization transfer amplitudes in the coupled nuclear spin system.
The figure shows a superconducting magnet which creates the magnetic field that aligns the nuclear spins. The liquid solution of the molecule with five coupled spins (see picture above) is located in the center of the magnet and forms the heart of the NMR quantum computer. We could also prove that the exact analogy between pendulums and TOCSY tranfer breaks down if more than three spins are part of the coupling network. Even for three spins, the exact analogy also only holds for the important case of "isotropic" coupling, which has the same form for all possible orientations of the frame of reference. Hence, it is an interesting open question whether classical analogies also exist for other types of spin-spin couplings, such as "dipolar" or "planar" couplings, for which the transfer dynamics is markedly different.
References:
- Spins Swing Like Pendulums Do: An Exact Classical Model for TOCSY Transfer in Systems of Three Isotropically Coupled Spins 1/2
R. Marx, S. J. Glaser, J. Magn. Reson. 164, 338-342 (2003). - Coherence Transfer by Isotropic Mixing: Application to Proton Correlation Spectroscopy
L. Braunschweiler, R. R. Ernst, J. Magn. Reson. 53, 521-528 (1983). - Geometrical representation of the schroedinger equation for solving the maser problem. R. P. Feynman, F. L. Vernon, R. W. Hellwarth, J. Appl. Phys. 28 (1957) 49-52.
Further reading:
- Homonuclear and Heteronuclear Hartmann-Hahn Transfer in Isotropic Liquids
S. J. Glaser, J. J. Quant, in: Advances in Magnetic and Optical Resonance Vol. 19, pp. 59-252 (1996), Ed.: W. S. Warren (Academic Press). - Analytical Coherence Transfer Functions for the General AMX System under Isotropic Mixing
O. Schedletzky, S. J. Glaser, J. Magn. Reson. A 123, 174-180 (1996). - Analytical Polarization and Coherence Transfer Functions for Three Coupled Spins 1/2 under Planar Mixing Conditions
O. Schedletzky, B. Luy, S. J. Glaser, J. Magn. Reson. 130, 27-32 (1998). - Analytical Polarization Transfer Functions for Four Coupled Spins 1/2 under Isotropic Mixing Conditions
B. Luy, O. Schedletzky, S. J. Glaser, J. Magn. Reson. 138, 19-27 (1999). - Analytical Polarization and Coherence Transfer Functions for Three Dipolar Coupled Spins 1/2
B. Luy and S. J. Glaser, J. Magn. Reson. 142, 280-287 (2000). - Superposition of Scalar and Residual Dipolar Couplings: Analytical Transfer Functions for Three Spins 1/2 under Cylindrical Mixing Conditions
B. Luy, S. J. Glaser, J. Magn. Reson. 148, 169-181 (2001). - Coupling Topology Dependence of Polarization-Transfer Efficiency in TOCSY and TACSY Experiments
S. J. Glaser, J. Magn. Reson. A 104, 283-301 (1993). - Tailored Correlation Spectroscopy for the Enhancement of Fingerprint Cross Peaks in Peptides and Proteins
Quant, T. Prasch, S. Ihringer, S. J. Glaser, J. Magn. Reson. B 106, 116-121 (1995). - Assessment and Optimization of Pulse Sequences for Homonuclear Isotropic Mixing
S. J. Glaser, G. P. Drobny, in: Advances in Magnetic Resonance, Vol. 14, pp. 35-58 (1990), Ed.: W. S. Warren (Academic Press). - A Theoretical Study of Coherence Transfer by Isotropic Mixing: Calculation of Pulse Sequence Performance for Systems of Biological Interest
M. L. Remerowski, S. J. Glaser, G. P. Drobny, Mol. Phys. 68, 1191-1218 (1989).
