
PENDEL SIMULIEREN SPINDYNAMIK
Quanten-Phänomene durch Spielzeuge begreifbar gemacht
Gekoppelte Pendel simulieren Quantenmechanik
Die Quantenmechanik gehört nicht gerade zu den leicht verständlichen Kapiteln der Naturwissenschaften. Doch jetzt haben zwei Forscher der TU München ein einfaches Modell entwickelt, das die wenig anschaulichen Gesetze dieser Disziplin »begreifbar« machen kann. Mit einfachen Metall-Pendeln stellen Prof. Steffen Glaser und Dr. Raimund Marx aus dem Institut für Organische Chemie und Biochemie in Garching magnetische Quantenphänomene nach. Sie benutzen mit Stahlfedern (bzw. bei einfachen Modellen mit Gummibändern) verbundene Metall-Pendel, um den Austausch von Magnetisierung zwischen den Kernspins von Atomen zu verstehen.

Mit Hilfe dieser Pendel erklärt Prof. Dr. Steffen Glaser Aspekte der Quantenmechanik.
Durch ihren Spin (oder Drall) werden Atomkerne zu kleinen Magneten. Der Austausch dieser Magnetisierung steht im Interesse der Wissenschaftler, da er eine entscheidende Rolle in der Kernresonanz-Spektroskopie spielt. Diese Technik gehört zu den modernsten Untersuchungsmethoden, mit denen Chemiker die räumliche Struktur von Molekülen entschlüsseln können. Die Wissenschaftler haben, wie das renommierte Journal of Magnetic Resonance berichtet, das Verhalten von drei magnetischen Kernspins durch die Schwingungen von drei gekoppelten Pendeln simuliert. Dies macht die Berechnung komplizierter Formeln oder die Simulation mit speziellen Computerprogrammen überflüssig. Solche mechanischen Modelle, von denen bisher nur sehr wenige für quantenmechanische Phänomene gefunden wurden, können dazu dienen, Studierenden die Gesetze der Quantenwelt verständlich zu machen. Außerdem helfen sie den Experten, einen intuitiven Zugang zur Quantenmechanik zu finden und so beispielsweise spektroskopische Methoden zu verbessern.
Bei der Suche nach quantenmechanischen Fällen, die sie mit den einfachen Pendeln simulieren können, stellten Glaser und Marx fest, dass die Vorhersage maximal für Systeme mit drei untereinander gekoppelten Spins funktioniert. Da bei mehr Spins die Quanten-Oszillationen viel komplexer werden als die mechanischen Schwingungen, lassen sich für größere Spin-Kopplungsnetzwerke mit dem einfachen »Spielzeug« keine Vorhersagen mehr machen. Das Modell ist aber keineswegs nur auf kleine Moleküle aus drei Atomen beschränkt. Denn komplexe Moleküle können mehrere voneinander unabhängige Atomgruppen mit je drei gekoppelten Kernspins enthalten. Das gilt beispielsweise für die drei Wasserstoff-Kernspins der Aminosäure Glycin in einem Protein. Da die Wasserstoffkerne jeder Aminosäure in einem Protein ein isoliertes Spinsystem bilden, kann das Pendelsystem das magnetische Verhalten etwa aller Glycin-Spinsysteme in einem bestimmten Protein simulieren, das insgesamt aus Tausenden von Atomen besteht.
Die Wissenschaftler haben ihr Modell zum Verständnis so genannter TOCSY-Experimente (TOtal Correlation SpectroscopY) genutzt, bei denen der Austausch von Magnetisierung zwischen Kernspins eine wichtige Rolle spielt. Diese spezielle Technik der Kernresonanz-Spektroskopie (Nuclear Magnetic Resonance, NMR) wurde von dem Nobelpreisträger Prof. Richard Ernst entwickelt, um die Struktur großer Moleküle mit Hunderten oder Tausenden von Atomen zu untersuchen. Mit Hilfe dieser Methode ist es möglich, jede der Tausende von NMR-Resonanzen eines Proteins einem bestimmten Atom des Proteins zuzuordnen. Dies ist eine wesentliche Voraussetzung, um schließlich die räumliche Struktur und dreidimensionale Faltung eines Proteins bestimmen zu können.
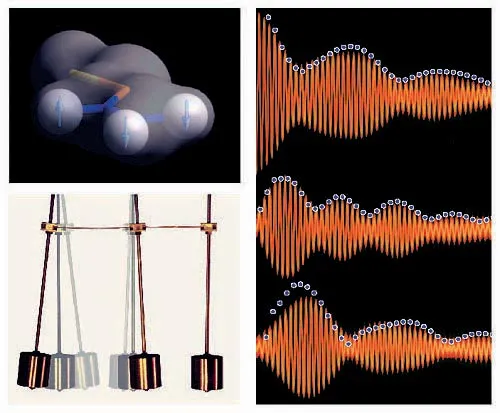
Kernspin-System, das durch die Wasserstoff-Atome des Moleküls Vinyl-
magnesiumbromid (schematisch oben links dargestellt) und der Energie-
Übertragung (rote Kurven) im entsprechenden gekoppelten Pendelsystem.
Exakte Analogien aus der klassischen Physik sind nur für wenige Quantensysteme bekannt. Ein berühmtes Beispiel stammt von Feynman, Vernon und Helwarth, die zeigten, dass jedes quantenmechanische Zweiniveau-System durch einen klassischen Kreisel exakt modelliert werden kann. Dies gilt zum Beispiel für die Kernspin eines Ensembles von isoliertenWasserstoffatoms in einem Magnetfeld.
Referenzen:
- Spins Swing Like Pendulums Do: An Exact Classical Model for TOCSY Transfer in Systems of Three Isotropically Coupled Spins 1/2
R. Marx, S. J. Glaser, J. Magn. Reson. 164, 338-342 (2003). - Coherence Transfer by Isotropic Mixing: Application to Proton Correlation Spectroscopy
L. Braunschweiler, R. R. Ernst, J. Magn. Reson. 53, 521-528 (1983). - Geometrical representation of the schroedinger equation for solving the maser problem. R. P. Feynman, F. L. Vernon, R. W. Hellwarth, J. Appl. Phys. 28 (1957) 49-52.
Weiterführende Literatur:
- Homonuclear and Heteronuclear Hartmann-Hahn Transfer in Isotropic Liquids
S. J. Glaser, J. J. Quant, in: Advances in Magnetic and Optical Resonance Vol. 19, pp. 59-252 (1996), Ed.: W. S. Warren (Academic Press). - Analytical Coherence Transfer Functions for the General AMX System under Isotropic Mixing
O. Schedletzky, S. J. Glaser, J. Magn. Reson. A 123, 174-180 (1996). - Analytical Polarization and Coherence Transfer Functions for Three Coupled Spins 1/2 under Planar Mixing Conditions
O. Schedletzky, B. Luy, S. J. Glaser, J. Magn. Reson. 130, 27-32 (1998). - Analytical Polarization Transfer Functions for Four Coupled Spins 1/2 under Isotropic Mixing Conditions
B. Luy, O. Schedletzky, S. J. Glaser, J. Magn. Reson. 138, 19-27 (1999). - Analytical Polarization and Coherence Transfer Functions for Three Dipolar Coupled Spins 1/2
B. Luy and S. J. Glaser, J. Magn. Reson. 142, 280-287 (2000). - Superposition of Scalar and Residual Dipolar Couplings: Analytical Transfer Functions for Three Spins 1/2 under Cylindrical Mixing Conditions
B. Luy, S. J. Glaser, J. Magn. Reson. 148, 169-181 (2001). - Coupling Topology Dependence of Polarization-Transfer Efficiency in TOCSY and TACSY Experiments
S. J. Glaser, J. Magn. Reson. A 104, 283-301 (1993). - Tailored Correlation Spectroscopy for the Enhancement of Fingerprint Cross Peaks in Peptides and Proteins
J. Quant, T. Prasch, S. Ihringer, S. J. Glaser, J. Magn. Reson. B 106, 116-121 (1995). - Assessment and Optimization of Pulse Sequences for Homonuclear Isotropic Mixing
S. J. Glaser, G. P. Drobny, in: Advances in Magnetic Resonance, Vol. 14, pp. 35-58 (1990), Ed.: W. S. Warren (Academic Press). - A Theoretical Study of Coherence Transfer by Isotropic Mixing: Calculation of Pulse Sequence Performance for Systems of Biological Interest
M. L. Remerowski, S. J. Glaser, G. P. Drobny, Mol. Phys. 68, 1191-1218 (1989).