ix-quadrat

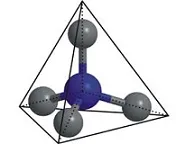
(blau: Stickstoff-Atom; grau: Wasserstoff-Atome).
der vier Wasserstoff-Kernspins im Ammonium-Ion.
Binomialverteilung: Murmelbahn und NMR
Mit der "rechnenden Murmelbahn" aus der Ausstellung ix-quadrat des Zentrums Mathematik an der TU München (Leitung: Prof. Richter-Gebert) lassen sich Binomialkoeffizienten "spielend" berechnen (PDF). In der Kernresonanz-Spektroskopie (engl: Nuclear Magnetic Resonance, NMR) folgen Signalintensitäten oft einer solchen Binomialverteilung. Dies soll hier am Stickstoff-Signal des Ammonium-Ions veranschaulicht werden.
Das Ammonium-Ion (NH4+) ist wie das Methan (CH4) tetraedrisch aufgebaut. Im Falle des Ammonium-Ions ist ein zentrales Stickstoff-Atom an vier Wasserstoffatome gebunden. Bestimmte magnetische Eigenschaften von Wasserstoff, Kohlenstoff und Stickstoff lassen sich mit Hilfe der NMR-Spektroskopie vermessen. Das Ergebnis einer solchen Messung ist ein Spektrum, bei dem unterschiedliche Atomkerne eines Moleküls Signale bei unterschiedlichen Frequenzen liefern.
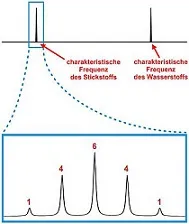
Das Spektrum des tetraedrisch aufgebauten Ammonium-Ions besteht, grob betrachtet, aus einem Signal bei der charakteristischen Frequenz des Stickstoffs und einem Signal bei der charakteristischen Frequenz des Wasserstoffs. (Tatsächlich liefert nur das seltene Stickstoff-Isotop 15N ein NMR-Signal.) Schaut man sich die Signale genauer an, stellt man fest, dass sie aus mehreren Einzelkomponenten bestehen. Wie das vergrößerte Bild des Stickstoff-Signals vom Ammonium-Ion zeigt, besteht dieses aus fünf Einzelkomponenten unterschiedlicher Intensität.
Diese Signal-Struktur wird durch die Wechselwirkung des Stickstoff-Atoms mit den vier gebundenen Wasserstoff-Atomen hervorgerufen. Die sogenannten Kernspins der Wasserstoffatome sind entweder nach oben oder nach unten ausgerichtet. Die genaue Frequenz der Einzelkomponenten des Stickstoff-Signals hängt von der Anzahl der nach oben ausgerichteten Wasserstoff-Kernspins ab.
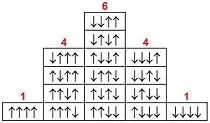
Die relative Größe der fünf Einzelkomponenten entspricht der jeweiligen Zahl der Kombinationsmöglichkeiten um eine bestimmte Anzahl nach oben ausgerichteter Wasserstoff-Kernspins zu finden. Beispielsweise gibt es nur eine Kombination, bei der alle vier Spins nach oben zeigen. Es gibt aber vier Kombinationen, bei denen drei Spins nach oben zeigen und sechs Kombinationen, bei denen zwei Spins nach oben zeigen etc. (siehe Abbildung).
Die resultierende Größe der Einzelkomponenten des Stickstoff-NMR-Signals entspricht gerade den Binomialkoeffizienten, die von der rechnenden Murmelbahn geliefert werden: 1:4:6:4:1.
Dr. R. Marx und Prof. S. Glaser (2005)