Quantencomputer und die Erkennung von Mustern
Vor Kurzem ist es uns gelungen ein neuartiges Quanten-Mustererkennungsschema zu erstellen, welches die Idee eines klassischen, neuronalen Hopfield-Netzwerkes mit der Idee eines adiabatischen Quantencomputers kombiniert. Im Gegensatz zu klassischen, neuronalen Netzwerken kann der Algorithmus eine Viehzahl erkannter Muster gleichzeitig als Ergebnis liefern. Der Ansatz verspricht auch eine Erweiterung der klassichen Speicherkapazität. Ein Gundsatzbeweis für den Algorithmus im Fall von zwei Qubits wird durch die Verwendung eines NMR-Quantencomputers erbracht.
Zusammen mit Wissenschaftlern von Siemens Corporate Technology (CT) ist es uns gelungen, eine erste experimentelle Implementierung eines künstlichen, neuronalen Netzwerkes auf einem einfachen Quantencomputer zu erreichen. Die Simulation einer Mustererkennung, die durch die CT-Wissenschaftler durchgeführt wurde, wurde mit einem Kernmagnetresonanz (nuklear magnetic resonance (NMR))-Spektrometer der TU München ausgewertet.
Die verwendeten Muster setzen sich aus Pixeln zusammen. Jedes Pixel kann zwei Farben übernehmen, welche durch Qubits bildlich dargestellt werden. Indem man einen Spezialalgorithmus verwendet, können Simulationen voraussagen, wie sich ein echter Quantenprozessor verhalten würde, wenn er mit einem neuen Farbmuster konfrontiert würde. Der Algorithmus vergleicht die Muster mit den gespeicherten Mustern und zeigt den Grad an Ähnlichkeit an.
Für die Experimente an der TU München wurde eine Natriumformiatlösung bei Raumtemperatur verwendet. Jedes Natriumformiatmolekül enthält ein Kohlenstoff- und ein Wasserstoffatom. In einem starken Magnetfeld, bildet jedes der beiden Partikel ein Quantenbit (Qubit). Die gemessenen Signale des Quantencomputers stimmten exakt mit den durch numerische Simulationen vorausgesagten Signalen überein.

Die einfachen gespeicherten Muster bestanden aus den Werten 1 (grün) und -1 (rot). Die linke Säule zeigt ein unvollständiges Eingabemuster. Die experimentell erkannten, vollständigen Muster (und ihre spektralen Signaturen) werden in der mittleren Säule für den Fall gezeigt, in dem die gespeicherten Muster (1,-1) und (-1,1) sind. Die rechten Säulen zeigen die Ergebnisse für den Fall, wenn die gespeicherten Muster (1,1) und (-1,-1) sind.

Rodion Neigovzen und Prof. Dr. Steffen Glaser im NMR-Labor, TU München.
Originalmanuskript:
quant-ph: Quantum Pattern Recognition With Liquid State NMR von R. Neigovzen, J. Neves, R.Sollacher, S. J. Glaser
Weitere Informationen zu dem Thema:
- Süddeutsche Zeitung - Wissen: Quanten, lest die Signale - 1, l oder I?
- ars technica: Quantum computer may be capable of seeing the big picture
- Siemens ResearchNews: Muster erkennen mit dem Quantencomputer
Weitere Veröffentlichungen im Bereich Quanteninformationsprozesse der Glaser-Gruppe:
- Optimal Control for Generating Quantum Gates in Open Dissipative Systems
T. Schulte-Herbrüggen, A. Spörl, N. Khaneja, S. J. Glaser
preprint: quant-ph/0609037. - The Significance of the C-Numerical Range and the Local C-Numerical Range in Quantum Control and Quantum Information
T. Schulte-Herbrüggen, G. Dirr, U. Helmke, S. J. Glaser
Lin. and Multilin. Alg. 56, 3-26 (2008). - Geodesics for Efficient Creation and Propagation of Order along Ising Spin Chains
H. Yuang, S. J. Glaser, N. Khaneja
Phys. Rev. A 76, 012316/1-6 (2007). Preprint (pdf) - Shortest Paths for Efficient Control of Indirectly Coupled Qubits
N. Khaneja, B. Heitmann, A. Spörl, H. Yuan, T. Schulte-Herbrüggen, S. J. Glaser
Phys. Rev. A 75, 012322/1-10 (2007). Preprint (pdf) - Optimal Control of Josephson Qubits
A. Spörl , T. Schulte-Herbrüggen, S. J. Glaser, V. Bergholm, M. J. Storcz, J. Ferber, F. K. Wilhelm
Phys. Rev. A 75, 012302/1-9 (2007). - Parallelising Matrix Operations on Clusters for an Optimal Control-Based Quantum Compiler
T. Gradl, A.K. Spörl, T. Huckle, S. J. Glaser, and T. Schulte-Herbrüggen
Proc. EUROPAR 2006, Parallel Processing Lecture Notes in Computer Science 4128, 751-762 (2006). - Non-Computing Applications of Quantum Information in NMR
S. J. Glaser, T. Schulte-Herbrüggen, N. Khaneja
Informatik Forsch. Entw. 21, 65-71 (2006). - Quantum Computing Implemented via Optimal Control: Theory and Application to Spin- and Pseudo-Spin Systems
T. Schulte-Herbrüggen, A. K. Spörl , R. Marx, N. Khaneja, J. M. Myers, A. F. Fahmy, S. J. Glaser
in Lectures on Quantum Information, Eds.: D. Bruß and G. Leuchs, pp. 481-501, Wiley-VCH (2006). - From Network Complexity to Time Complexity via Optimal Control
T. Schulte-Herbrüggen, A. Spörl, N. Khaneja, S. J. Glaser
NATO Science Series,III: Computer and System Sciences 199, 353-357 (2006). - Relaxation Optimized Transfer of Spin Order in Ising Chains
D. Stefanatos, N. Khaneja, S. J. Glaser
Phys. Rev. A 72, 062320/1-6 (2005). Preprint (pdf) - Optimal Control-Based Efficient Synthesis of Building Blocks of Quantum Algorithms Seen in Perspective from Network Complexity towards Time Complexity
T. Schulte-Herbrüggen, A. Spörl, N. Khaneja, S. J. Glaser
Phys. Rev. A 72, 042331/1-7 (2005). Preprint (pdf) - Increasing the Size of NMR Quantum Computers
S. J. Glaser, R. Marx, T. Reiss, T. Schulte-Herbrüggen, N. Khaneja, J. M. Myers, A. F. Fahmy
in: Quantum Information Processing, pp. 53-65, Eds.: G. Leuchs, T. Beth (Wiley-VCH). - Broadband Geodesic Pulses for Three Spin Systems: Time-Optimal Realization of Effective Trilinear Coupling Terms and Indirect SWAP Gates (81)
T. O. Reiss, N. Khaneja, S. J. Glaser
J. Magn. Reson. 165, 95-101 (2003). Preprint (pdf) - Sub-Riemannian Geometry and Time Optimal Control of Three Spin Systems: Quantum Gates and Coherence Transfer
N. Khaneja, S. J. Glaser, R.
Brockett Phys. Rev. A 65, 032301 (2002). - Efficient Transfer of Coherence Through Ising Spin Chains
N. Khaneja, S. J. Glaser
Phys. Rev. A 66, 060301(R) (2002). - Geometry of Quantum Computing by Hamiltonian Dynamics of Spin Ensembles
T. Schulte-Herbrüggen, K. Hüper, U. Helmke, S. J. Glaser
in: Applications of Geometric Algebra in Computer Science and Engineering, L. Dorst, C. Doran and J. Lasenby, Eds., Birkhäuser, Boston, 269-281 (2002). - Cartan Decomposition of SU(2n), Constructive Controllability of Spin Systems and Universal Quantum Computing
N. Khaneja, S. Glaser
Chem. Phys. 267, 11-23 (2001). - Time Optimal Control in Spin Systems
N. Khaneja, R. Brockett, S. J. Glaser
Phys. Rev. A 63, 032308 (2001). - NMR Quantum Computing
S. J. Glaser
Angew. Chem. Int. Ed. 40, 147-149 (2001); Angew. Chem. 113, 151-153 (2001). - Rapid Solution of Problems by Nuclear Magnetic Resonance Quantum Computing
J. M. Myers, A. F. Fahmy, S. J. Glaser, R. Marx
Phys. Rev. A 63, 032302 (2001). - Chemical Enigneering of an NMR Quantum Computer
R. Marx, A. F. Fahmy, J. M. Myers, W. Bermel, S. J. Glaser
in: Quantum Computing, Eds.: E. Donkor and A. R. Pirich, Proceedings of SPIE Vol. 4047, pp. 131-138 (2000). - Nuclear Magnetic Resonance Quantum Computing Exploiting the Pure Spin State of Para Hydrogen
P. Hübler, J. Bargon, S. J. Glaser
J. Chem. Phys. 113, 2056-2059 (2000). - Approaching Five-Bit NMR Quantum Computing
R. Marx, A. F. Fahmy, J. M. Myers, W. Bermel, S. J. Glaser
Phys. Rev. A 62, 012310 (2000). - quant-ph/9905087 press reports Unitary Control in Quantum Ensembles, Maximizing Signal Intensity in Coherent Spectroscopy
S. J. Glaser, T. Schulte-Herbrüggen, M. Sieveking, O. Schedletzky, N. C. Nielsen, O. W. Sørensen, C. Griesinger
Science 280, 421-424 (1998). (Abstract and additional information)

Kernspinresonanz (NMR) Spektrometer an der TU München
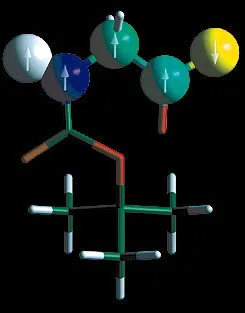
Molekulare "hard ware" des ersten 5-Qubit-NMR-Quantencomputers. Vorabdruck: quant-ph/9905087 press reports